Kaleidoscope Pro allows you to quickly sort, label, and identify bird songs, frog calls, and bat identifications from weeks, months, or even years of recordings.
Subscription allows two activations for a single user for 12 months upon activation. Non-refundable.
University pricing is available, contact sales for details.
For larger quantities, contact sales2023@wildlifeacoustics.com
Whether you’re conducting species inventory, presence/absence surveys, endangered species detection or habitat health monitoring, Kaleidoscope Pro significantly minimizes the time it takes to find what you’re looking for.
Subscription Credits: Kaleidoscope Pro is available through the purchase of a subscription credit. A credit, when activated in the Kaleidoscope program, gives you access to Kaleidoscope Pro for a 12-month period for one user across two devices. A credit can be applied to a new subscription or to renew an existing subscription. Credits do not expire. If needed, you may purchase multiple credits for a multi-year project at a single time and reserve unused credits until you need them..
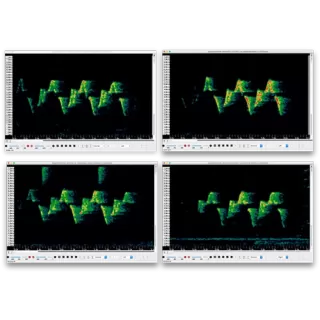
Kaleidoscope Pro’s Cluster Analysis uses sophisticated pattern recognition algorithms to automatically scan wildlife audio recordings for bird songs, frog calls, bat echolocations, or other animal vocalizations. Once detected, the sounds are sorted into groups of similar sounds called “clusters.” Clusters can be labeled for species inventory or annotated to create classifiers that can be run on additional recordings.
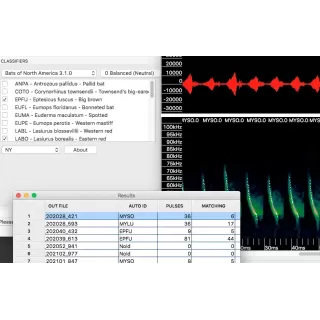
Kaleidoscope Pro Bat Auto-ID analyzes recordings of bat echolocations and automatically suggests the most likely bat species around you.* The software also provides an efficient workflow for manually vetting Bat Auto-ID suggestions, reducing the amount of time necessary to analyze your recordings.
*Bat Auto-ID classifiers are currently available for North America, Europe, South America, and the Neotropics.
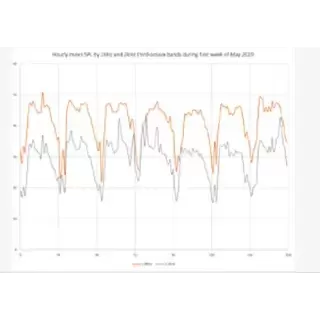
The Kaleidoscope Pro Sound Level Analysis feature allows you to scan a batch of recordings in accordance with various standards to analyze the noise spectrum and generate a report. Analysis includes weighted SPL and SEL measurements as well as third octave band analysis.
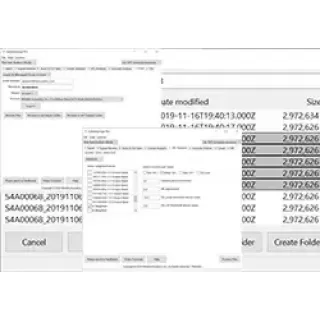
Cloud computing lets you borrow a supercomputer in the cloud. Quickly search your recordings to find exactly what you're looking for. Store recordings in our secure cloud for safe backup, collaborate with others, and automatically emails for when the results are ready.
Our new Facebook group, Kaleidoscope Connect, is dedicated to helping Kaleidoscope Pro users understand Cluster Analysis. Share settings, tips and tricks, and ask other users for advice and guidance. Check it out today!
Join our mailing list to get notified about upcoming training opportunities, important technical service bulletins, webinars, our quarterly grant program, and product updates.
Thank you for signing up to our mailing list.
You can unsubscribe or change your email settings at any time by clicking "Manage Preferences" link at the bottom of any mailing list emails we send you.
Wildlife Acoustics, Inc.
3 Mill and Main Place, Suite 110
Maynard, MA 01754-2657 USA
+1 (978) 369-5225
+1 (888) 733-0200